目录
- 基于计数器的限流
- 基于滑动窗口的限流
- 基于漏桶算法的限流
- 基于令牌桶算法的限流
基于计数器的限流
计数器算法是限流算法中最简单和最常见的一种。它基于一个计数器来跟踪一段时间内处理的请求数。如果请求次数超过了预设的阈值,新的请求将被拒绝或排队等待处理。
比如希望限制系统每分钟处理的请求数量为 100 次,那我们只需要在内存中维护一个计数器,每次来一个请求,就对这个计数器*+1*,另外每过一分钟,也会定时把内存中的计数器清零。
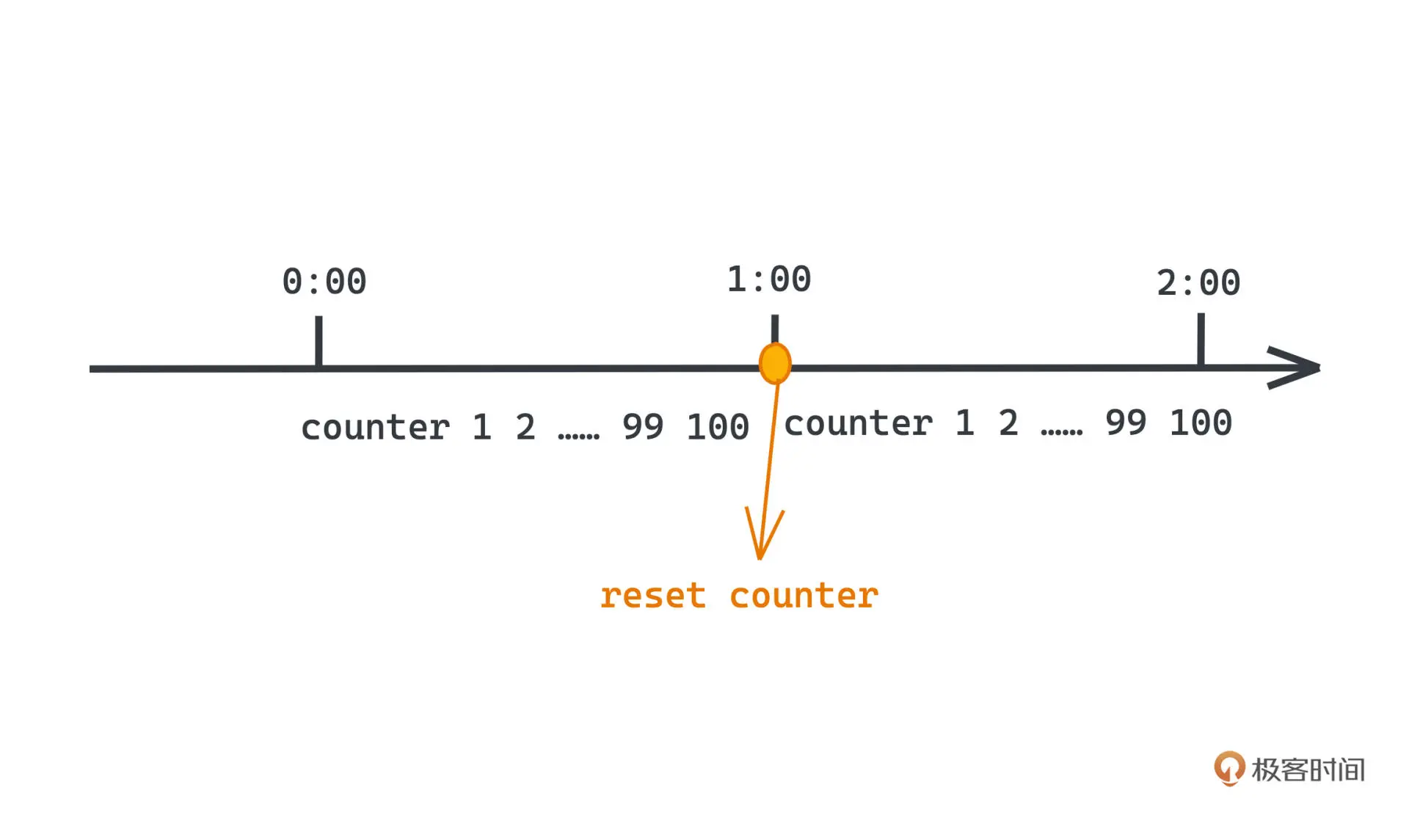
当请求来的时候,如果发现计数器的值已经超过 100 次,就会直接拒绝这次请求。这样我们就可以严格地控制每分钟内的请求都不会超过 100 次了。
这个方法简单粗暴,但有一个很大的问题,那就是 临界问题 。我们没法细粒度地控制流量在定时区间内的平滑性,如果遇到突发流量,可能会瞬间压垮我们的系统。
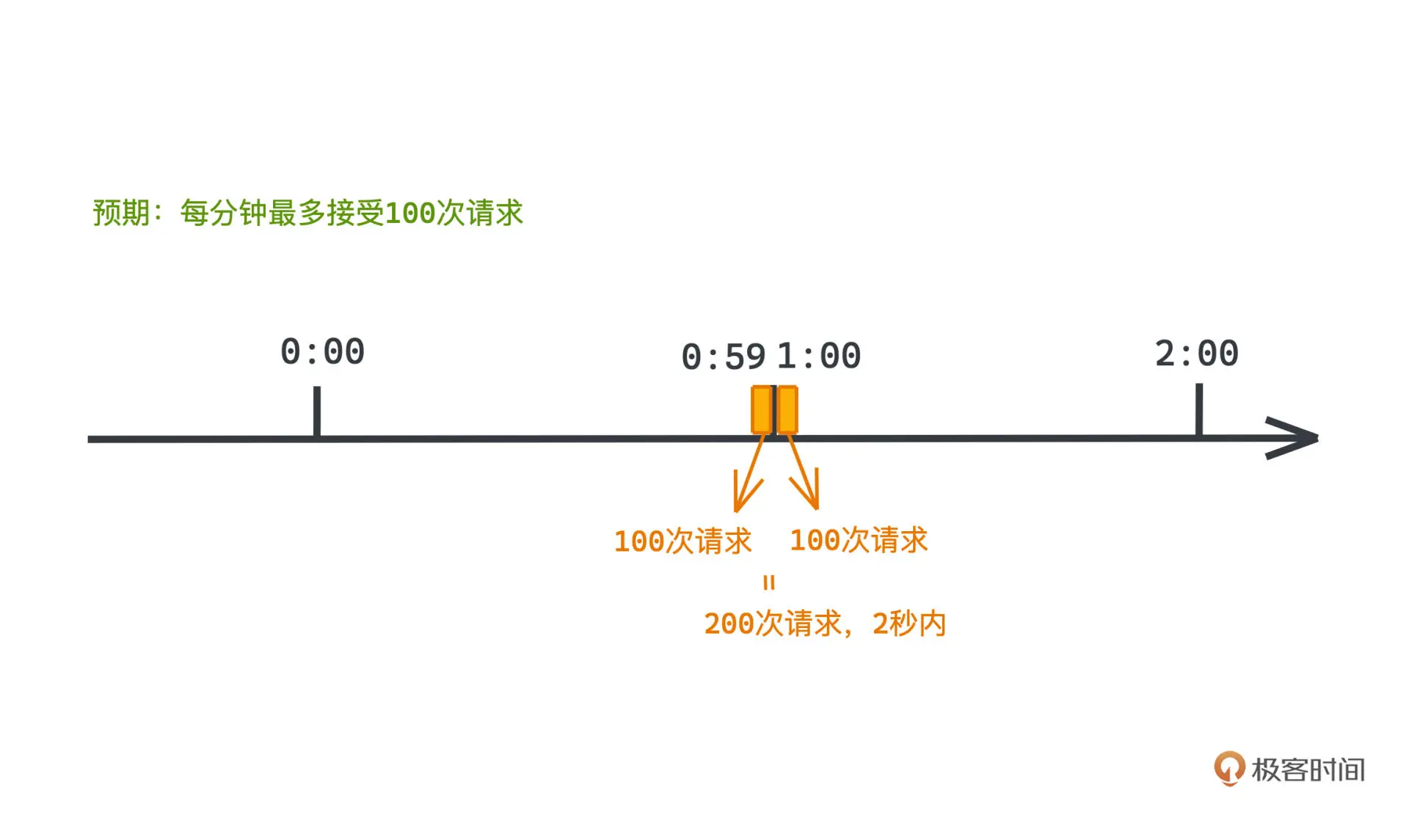
在每分钟 100 次请求的限流器中,如果在第1分钟的第 59 秒来了 100 个请求,在第2分钟开始的第 1 秒内又来了100个请求,也就是说在时间窗口重置节点处可以瞬间超过我们的速率限制,这显然不符合我们设计的初衷。
基于滑动窗口的限流
在上面提到的计数器算法中,比如限制每分钟处理的请求数为 100 次,那么这个1分钟就是一个固定的时间窗口。在固定窗口中,如果请求集中在时间窗口的临界处,则容易导致流量超过系统负载阈值。滑动窗口算法是将时间窗口划分为更细的时间周期,每次向右滑动一个周期来统计请求数是否超过阈值。
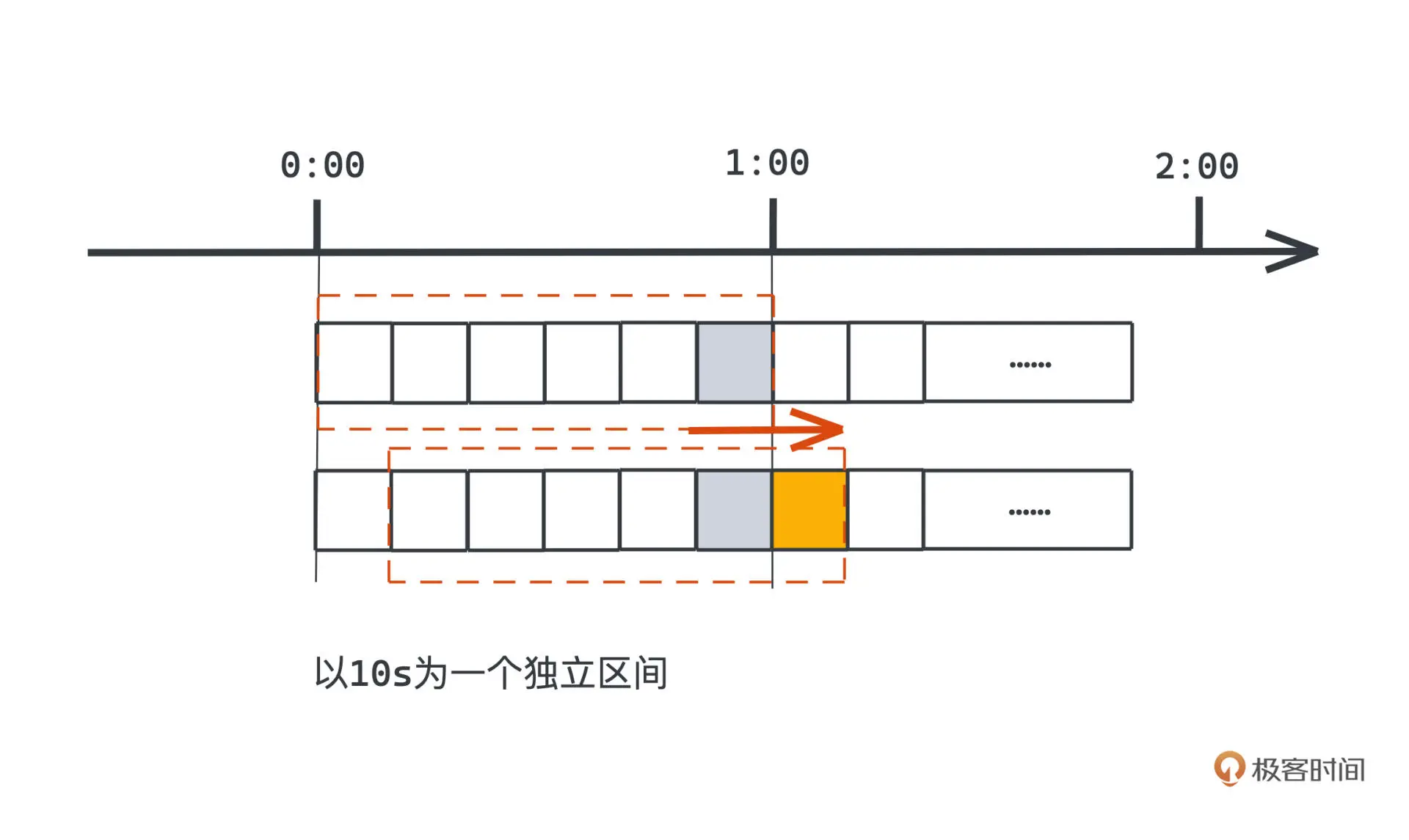
以分钟为单位统计访问次数粒度太粗,我们可以把统计计数器的区间变小一些,比如以 10 秒为一个区间,每个区间独立统计落在区间内的请求数量。我们遍历过去一分钟内每个独立区间,也就是每 10 秒内的计数器的计数总和,这个总和就是过去一分钟内全部的请求数量。每次经过 10 秒,我们自然需要把整个计数区间往右边移动一格。在图中的体现就是,当时间经过 1:00 的时候,整个限流器的计数器范围就去掉了最左边 0:00 - 0:10 的区间,增加了橙色的格子,也就是 1:00 - 1:10 的区间,这样的过程也就是我们通常所说的”滑动窗口”了。
在这个思路下,想要进一步提高被控制流量的平滑性就需要不断增加窗口的精度,也就是缩小每个区间的大小,但这样也会带来更多的内存开销,那有没有什么更好的方式可以帮助我们获得理论上更平滑的流量控制能力呢?
基于漏桶算法的限流
漏桶算法就是这样一种非常平滑的流控方式,它可以严格控制系统处理请求的频率。漏桶也就是 leaky bucket,本质就是用计算机模拟一个有漏洞的水桶,只要漏桶中有水存在,水桶的漏洞处就会稳定的有水流漏出。我们的请求,就像是一个往水桶里不断加入水的水管,水管的流量自然是可以有波动的,可以时快时慢,当漏桶已经被装满的时候,拒绝请求就可以了,就像让水不溢出一样。
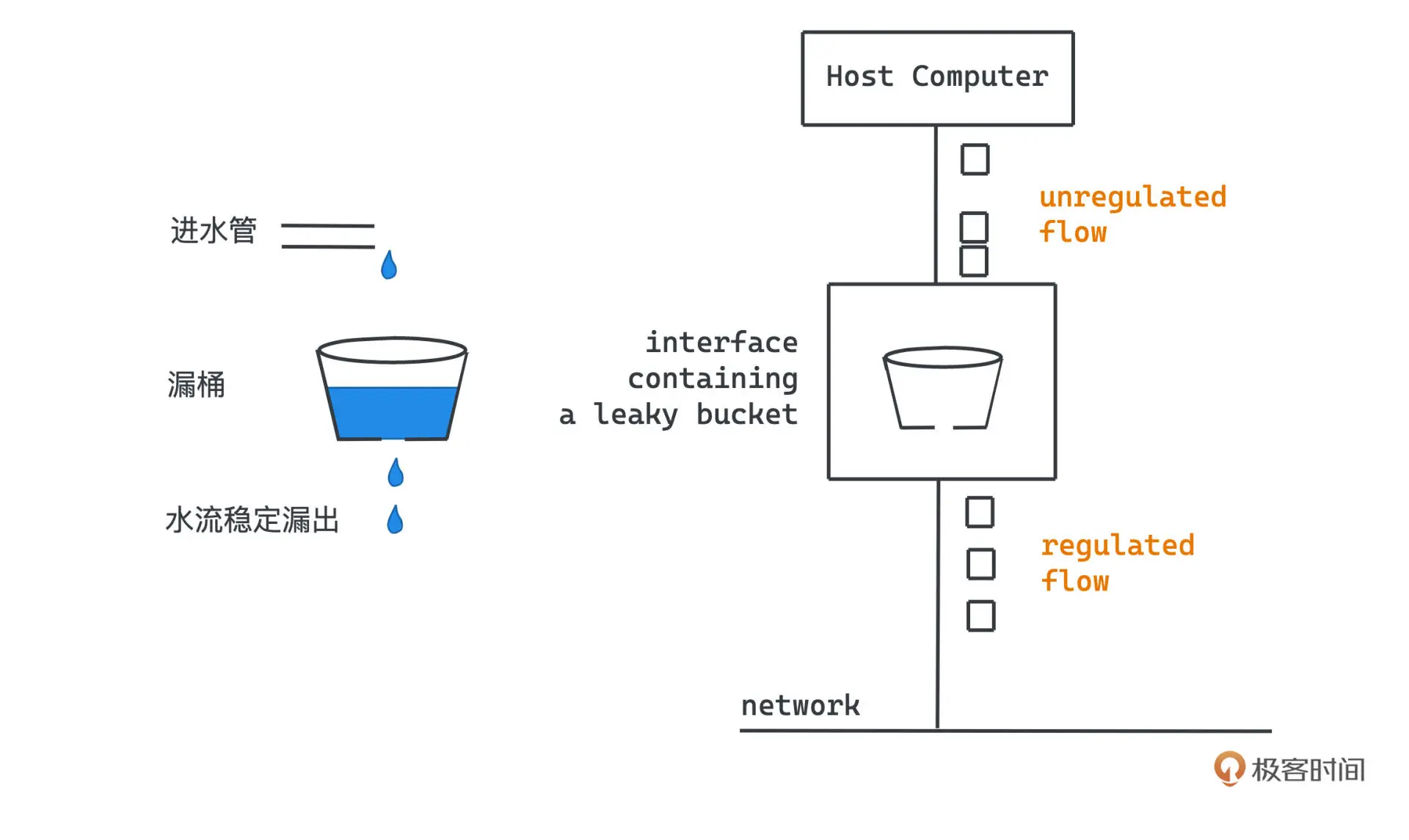
只要我们能让漏洞漏水的消费速度可控、稳定,整个系统只处理漏桶漏出的稳定流量,自然就可以达到限流的效果。
具体如何实现呢?漏桶最简单的一种实现正是基于队列。我们用一个 FIFO 队列模拟水桶,队列的容量就是水桶的最大大小。每来一个请求,就存储到队列中,如果队列满了,就直接拒绝。而另一侧,我们会有一个线程稳定消费队列中的数据,这样,整个系统不管在请求流量多么不稳定的情况下,都可以维持一个非常稳定的流量处理速度。
那漏桶算法有没有什么问题呢?漏桶这样严格完美的流量限制策略,也使得它完全放弃了应对突发流量的能力,因为在遇到突发流量时,漏桶的处理和平时并没有区别。很多时候我们也希望在面对突发流量的时候,系统可以稍微提高一下自己的处理速度,以获得更好的用户体验。有没有什么办法呢?
基于令牌桶算法的限流
和漏桶一样,令牌桶也采用了桶的模型,不过不同的是,我们不再是让系统处理定速从漏桶中流出的流量,而是改成把令牌以稳定的速度放入桶中。桶中令牌数会有一个上限,所以如果令牌桶已经被放满,多余的令牌不会被继续放入了。每来一个请求,必须先去令牌桶里申请令牌,申请到令牌的请求才能被服务器处理,否则,我们也会拒绝对应的请求。
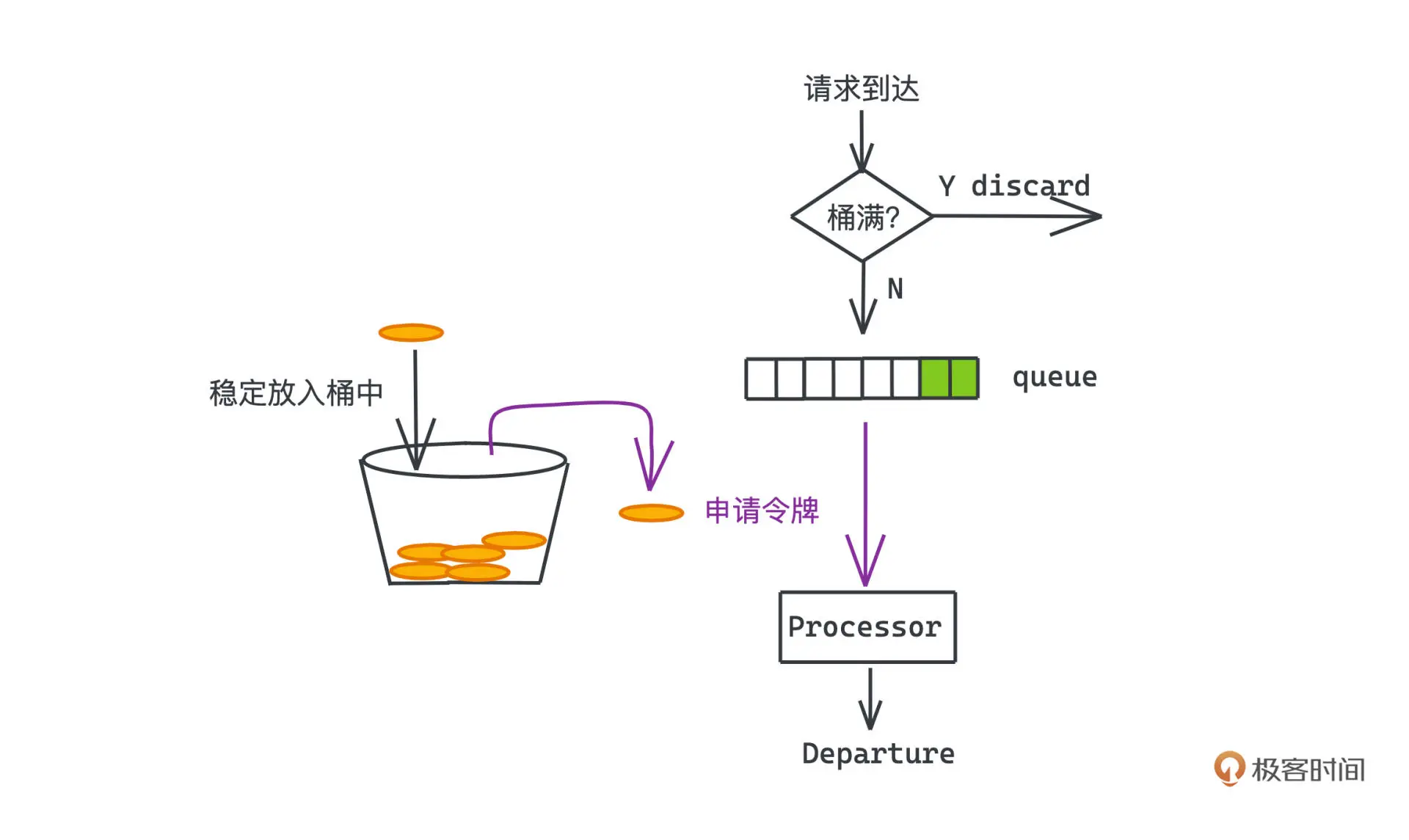
这个方案流量限制的核心就在于:令牌桶中令牌的数量是有限的。如果在一段时间内,请求的速度都是高于令牌放入的速度,令牌桶中很快就会没有令牌可用了,服务就会拒绝一部分请求,并保证系统处理的流量在我们的控制范围内。对比漏桶,令牌桶在请求流量低的时候,令牌数会慢慢增加直到放满,那么在遇到突发流量时,通常令牌桶内会有一定的令牌数,在这个限度内的请求,即使短时请求速度很快,我们也不会拒绝对应的请求,这就保证了我们在控制流量的同时,也有了一定的突发流量的应对能力。
基于同样的道理,令牌桶自然也可以基于队列实现。用队列存储令牌,每来一个请求就从队列中取出一个令牌,队列为空的时候则拒绝请求,另一边用一个线程稳定的向队列里放入令牌,在队列满的时候停止放入即可。
不过事实上,我们不需要真的在内存里维护这样占据内存空间的队列,可以采用计算时间的方式来模拟这个过程,核心思路就是既然我们知道令牌放入的速度,那完全可以通过上一次请求到达的时间和这次请求到达的时间差,判断请求来之前我们又多出来的可用的令牌数量。